Ali S. Fayad, Discoverer of The Explicit Alternate Flow Depth in Rectangular Open Channels

DSMS

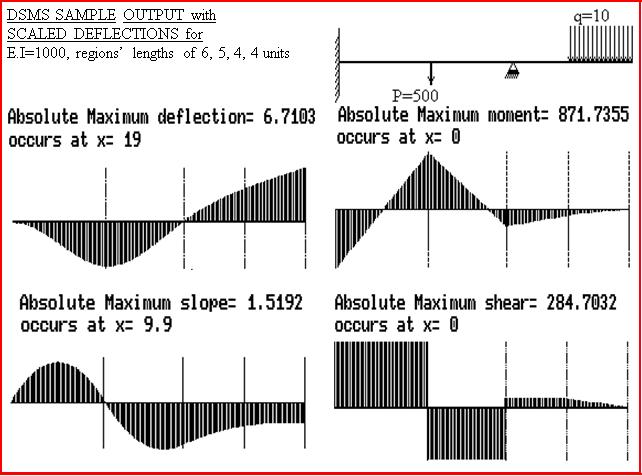
1.2 Deflection, Slope, Moment, & Shear:

Deflection, Slope, moment, and shear (DSMS) diagrams are essential in the design of structural members. Through their use the designer can often visualize the nature of the problem. Displaying graphs of these quantities on a microcomputer necessitates computations at a large number of points. The stiffness method of structural analysis is one means of providing the designer with these values, but it is restricted by its own definitions. Its mathematical methodology is based on the computation of values at the nodal points of the structure. A designer interested in values of DSMS between the nodes may become frustrated since such data has to be indirectly computed.

Thence stems the need for programs based on a mathematical approach that provides the designer with DSMS diagrams at any location in the structure. The accomplishment of such a task is provided by polynomials since they can describe the variation equation of a structural design parameter for every point in a structure. Many programmers complement their stiffness algorithms with computational tools that handle and plot polynomials. The direct solution for the coefficients of the DSMS polynomials, without the use of stiffness analysis, has been the methodology used in the continuous beam routines of DSMS (since 1986).

The polynomial approach manipulates the DSMS functions, through closed-form integration and differentiation; and models all types of supports including plastic moment hinges and shear hinges for continuous beams. This includes beams supported by columns or semi-rigid supports. DSMS simulates the formation of plastic hinges, and displays the redistribution of the moment and the corresponding changes in curvature and other quantities. This is possible because the engineer can specify the internal moment. Similarly, the designer can specify support settlement and non-rigid connection rotation.

1.3 Discontinuity in a Beam Model:

The beam may have a discontinuity because it has changed its geophysical characteristic or because of a concentrated effect such as a point load. The presence of stress irregularities within a non-traditional beam region is considered a discontinuity region such as may occur near a support. Currently, the program concentrates the effects of a discontinuity region into a single point in the form of defined concentrated effects that mathematically introduce abrupt changes into the beam model essentially dividing it into several regions.

1.4 Region Based Method

DSMS solves the beam equation in a different way than traditional stiffness method programs. Unlike traditional structural programs, DSMS analytically controls the solution to the problem. The solution that is obtained is a unique set of mathematical equations that exactly conforms to constraints and loads on the continuous beam. It obtains a region specific solution, in the form of polynomials that matches the characteristic functions of the beam as they are integrated and differentiated. A more detailed explanation of how this works is in the Structural Analysis section of the DSMS Reference Manual.

5. Model Information

Originally, and upon its inception in 1986, DSMS expected answers to boundary conditions at each region of continuity of the beam. This remains the means and ways by which its basic computational engine analytically controls the formulation of the model solution. Pre-processors and post-processors were added to change the questions to a more natural mode. This was eventually incorporated into the overall program and maintained. DSMS’ initial method of collecting information on the structural model has been maintained since the year of its copyright registration in 1987.

This consists of a query of the Quintessential Questions (QQs) that User must respond to in order to communicate the basic information to the machine. Over time, additional opportunities to make changes after a model is formulated in the computer were added.

DSMS, and other routines of Mnemosyne Fayad employing DSMS, collect structural information about the beam model from:
-User input: Examples of this type of information include the number of regions of continuity in the beam; length of each region; type of concentrated effects; and type along with values of the loads attached or applied to the beam.
-Initial defaults within the program: Examples of these defaults are, unit loads, baseline constraints, and other geometric and material properties.
-Internal libraries: includes information relating to steel, concrete, and timber construction material (currently available in other routines of Mnemosyne Fayad but not in DSMS itself)
-Progressive elaborations: information that is deemed essential to the program throughout the history of usage of DSMS (from 1986 to the present)

5.1 Information Exchange among Modules
The program prepares a disk-writable data file from the information that is obtained (per section “10.1 Model Information Collection”). Once User is at the {Completed Model Menu}, and opts to compute, the program writes the collected beam properties data to the disk. This allows the computational engine of the program to “do the math” and find the DSMS answers to the problem. Thence, there are always two distinct information sets on the model. The first is stored internally within the logic of the program pursuant to the input it receives from User. The 2nd is the beam properties data which is the succinct information that is processed by the computational engine as its input data. Output information is treated separately and is discussed elsewhere (see section 10.7 {Model Graphs Menu})

Information is shared within various modules of the program. It is assembled, as described above, for the following purposess:

-Comply with reality-checks and/or solid mechanics theory requirements
-Provide the DSMS solutions
-Offer User additional information related to the input and output
-Conduct preliminary construction cost estimates (currently available in other routines of Mnemosyne Fayad but not in DSMS)

5.2 Regional Continuity & Compatibility
Information is internally stored as data that gets prepared per User’s responses to QQs. It remains resident in computer memory until it is eventually written to the storage device. The data file stores boundary conditions between regions and information regarding the nature of their connection to the ground (the reference horizon). The respective loads are mathematically affiliated with their intended regions by their sequence as load polynomials. Each continuous region of the model must be compatible with the one next to it unless an inputted discontinuity (by User) supersedes the default continuity. These discontinuities can be manifest in the connection of one region to the other, in the connection to the ground, in geophysical properties of the regions, or through the imposed loads. Decisions on these boundary conditions are not final. Users, when selecting the Modify & Check option (see section “9.6 {Completed Model Menu}”), will be able to change these values. Here, the theme consists of a line of questions that the computer asks from User (the input questionnaire). If unable to understand these questions, User needs to improve familiarity with structural terminology before proceeding.

5.3 Method of Imposing Changes to Model
Insure that every region is indexed with its concentrated effects and loads on the beam prior to modeling. Currently, if User makes an input using inconsistent units, the units will not be converted (unless specifically noted in the input and output of other routines of Mnemosyne Fayad). A general unit conversion program may be used simultaneously with DSMS to convert values prior to input. Otherwise, User-to-program input must be in consistent units for a meaningful result.

Web Hosting by Turbify