Ali S. Fayad, Discoverer of The Explicit Alternate Flow Depth in Rectangular Open Channels

The maximum flow for the same specific energy value occurs at the critical depth. The relationship between the critical flow and its critical depth is: qc^2 = g.yc^3.

If the gate is closed (i.e., downstream-y = 0), then Mnemosyne plots various flows by using the given upstream depth as a hydrostatic depth. Mnemosyne permutes it as the specific energy available for various values of flow depths between the hydrostatic depth and zero. If the gate is open (i.e., downstream-y > 0), then Mnemosyne plots various flows by permuting the specific energy for the given flow condition between the corresponding hydrostatic depth and zero.  The resulting "Depth vs. Flow" curve gets smoother and more precise as the plot employs more data points. This is typically referred to as “discretization”. The above graph was based on a 10 point discretization.


Minimum Specific Energy:

The critical flow depth is said to occur, in an open channel, once the specific energy of the flow is at its minimum value. This depth can be derived mathematically by taking the derivative of the energy equation with respect to the Froude number and setting the result to zero.

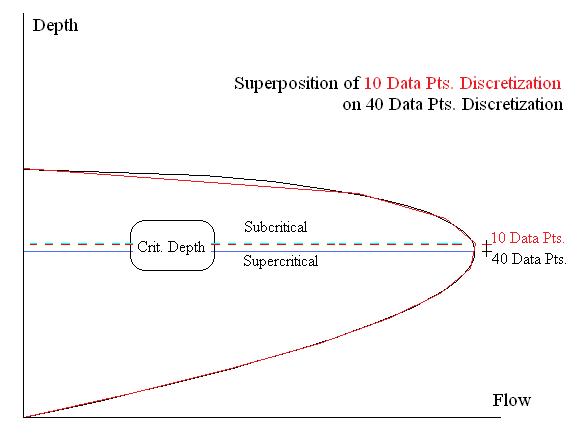
Mnemosyne's graphs are dependent on the extent of discretizaton. The superposition of different data-points graphs illustrates the significance of discretization on the result that is obtained. This is particularly true in the hydraulic profiling of gradually varied flow and rapidly varied flow. The graph’s poignancy is as a reminder of the tenuous nature of maintaining an exact critical depth flow regime in an open channel.